Click here for some current news and introduction in english

채널코드(Error-correcting Codes)와 PN코드(Pseudo-Noise Sequences)를 중심으로
디지털 통신 신호의 수학적 특성을 다루는 분야에서 다양한 연구과제를 수행하고 있습니다.
여기에 동참할  열정을 가진 지원자를 기다립니다.

송홍엽교수와 면담을 원한다면 hysong@yonsei.ac.kr  혹은 01076614861 혹은 카카오톡 hysong2013 으로 연락하기 바랍니다.
면담시 학부 성적증명서를 지참하면 도움이 됩니다.

박사과정은 등록금 전액과 추가의 급여를 지원하며, 석사과정은 연구비 상황에 따라 등록금의 일부 또는 전부를 지원합니다.

web counter
Hit Counting from June 1, 2015  

-----------------------------------------------------------------------------

 

2022-2 전기전자 선형대수 과목소개 자료

Preview of what we will study in this class - a short video on youtube

-----------------------------------------------------------------------------------

Error-Correcting Code (채널코드 혹은 오류정정부호) 연구의 주 목적은 디지털 통신 시스템의 신뢰도를 높이기 위하여 간단하면서도 강력한 코드를 찾고 이를 인코딩/디코딩하는 알고리즘을 설계하는 것입니다.
이는 안테나 키우기, 안테나 수 늘리기, 송신전력 키우기, 등등의 물리적인 방법이 한계에 다다라서
더 이상의 효과를 얻지 못하는 경우에도 좋은 효과를 얻을 수 있는 방법입니다.

 

추가 관련링크

오류정정부호의 응용에 관한 편집자의 글  (한국통신학회 학회지 정보와통신, 2015년 6월) 

채널코딩의 발전 과정 및 현재 상황  (Tutorial Article, 2009)

디지털통신과 오류정정부호 이야기, (송홍엽교수의  정보통신 따라잡기, 연세춘추, 1429호, 2001년 11월)

정보이론의 관점에서 소개하는 디지털 통신이론  (Tutorial Paper, 2000)

자신의 약점을 찾아서 - 유학생활과 오류정정부호 전공분야 소개  (첫눈에 반한 공과대학, 김영사, 1999)

 

최근 우리 연구실은 CLOUD 등의 분산 저장매체를 위한 Local Code 연구에서 좋은 결과를 많이 얻었습니다.
Graph 이론과의 밀접한 관계를 규명했으며 새로운 좋은 code를 개발하였습니다.

--------------------------------------------------------------------------------------

    PN sequences (랜덤코드, PN 코드) 설계의 주 목적은
    매우 간단한 알고리즘으로 랜덤한 특성을 가지는 수열을 만들어내기 위한 다양한 기법을 찾는 것입니다.
    이러한 특성의 PN코드는 다양한 이동/위성/무선통신시스템은 물론이고, GPS, Galileo등의 위성항법시스템,
    그리고 레이다 및 소나 등의 추적시스템에서 최고의 성능을 보장합니다.

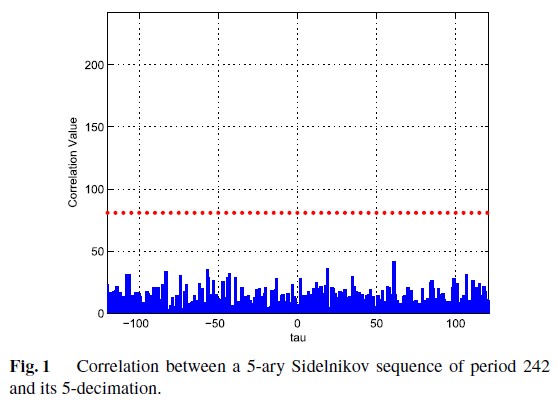
    예를 들어, 아래 그래프는 5-ary Sidelnikov sequence of length 242와 이것의 5-decimation sequence와의 상관 특성을 보여줍니다. 

    -----------------------------------------------------------------------------------

     

    최근, 본 연구실에서는 "완벽한 상관함수"를 가지는 신호집합을 생성하고, 이를 증명하는데 성공했습니다
    [2015년 6월 IEEE International Symposium on Information Theory 발표]. 
    이를     Fermat-Quotient sequence라고 부릅니다.

    약 50여년 전에 발표된 Frank-Zadoff sequence 와 밀접한 관계가 있음을 밝혀냈고,
    약 40여년 전 발표되었던     Zadoff-Chu sequence와는 길이와 성분면에서 완전히 다른 새로운 결과입니다.
    즉, 40여년 만에 전혀 새로운     완벽한 상관특성의 신호집합을 찾은 결과입니다.

    여기서 완벽한 상관함수란 자기상관특성이 완벽하다는 뜻으로, out-of-phase에서 자기상관값이 "0"임을 뜻합니다. 

 

---------------------------------------------------------------------------------------

...그 밖에...

 

 

    송홍엽교수의 특별한 관심 분야는 이산수학(Discrete Mathematics)의 한 분야인
    조합수학(Combinatorial Mathematics)    분야와 응용입니다.
    이 분야의 잘 발전된 순수이론은 위에서 설명한 모든 분야에 대한 다양한 이론적 배경을 형성합니다.

    조합수학 분야의 효시는 18세기 L. Euler가 최초로 발표했다는
    소위 "Euler Squares" 혹은 "Pair of Orthogonal Latin Squares"에 대한 연구로부터 시작하는 것으로 알려져 있습니다.
    Euler는 Magic Square (마방진)를 만드는 방법으로서 이를 연구했습니다.
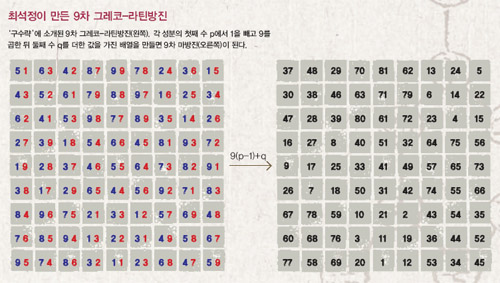
    예를 들어 아래 그림은     9x9  pair of orthogonal Latin square와
    이로부터     9x9  Magic Square를 만드는 과정을 보여줍니다.
    마방진은 모든 가로합, 세로합, 대각선합이 동일하다는 특징으로 정의됩니다.

    18세기 유럽의 L. Euler가 이러한 개념을 처음 생각한 것으로 알려져왔지만,
    그보다 최소한 60여년 앞서서 17세기 조선 숙종 시대에 영의정을 지낸 천재 수학자 최석정의 저서 "구수략"에  위의 그림이 표시되어 있습니다.
    놀랍지 않은가요?
    이러한 공적으로 인하여 2013년 대한민국 과학기술 명예의 전당에 수학자 최석정 선현이 헌정 되었고,
    송홍엽교수는 2017년 가을에 대한수학회 공로상을 수상했습니다.

    관련링크

This is the lecture in Youtube of my talk in the opening ceremony of Choi-Seok-Jeong Lecture Hall at KAIST in Sept. 7, 2018.